Question

In order to estimate the average time spent on the computer terminals per student at a local university, data were collected from a sample of 81 business students over a one-week period. Assume the population standard deviation is 1.2 hours. Calculate the margin of error (to two decimals) for a confidence interval with a confidence coefficient of 0.95.

Answer 1

Margin of error for a 95% of confidence intervals is 0.261

Explanation:

Step1:-

Sample n = 81 business students over a one-week period.

Given the population standard deviation is 1.2 hours

Confidence level of significance = 0.95

Zₐ = 1.96

Margin of error (M.E) =
`(Z_(\alpha )S.D )/(√(n) )`

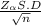
Given n=81 , σ =1.2 and Zₐ = 1.96

Step2:-

`Margin of error (M.E) = (Z_(\alpha )S.D )/(√(n) )`

`Margin of error (M.E) = (1.96(1.2) )/(√(81) )`

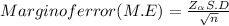
On calculating , we get

Margin of error = 0.261

Conclusion:-

Margin of error for a 95% of confidence intervals is 0.261