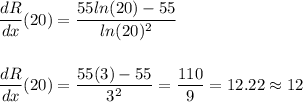Question

If the demand equation (in dollars) for a certain commodity is p = 55/ln x, where x represents the number of units of the commodity, determine the marginal revenue function for this commodity, and compute the marginal revenue when x = 20. What is the marginal revenue function for this commodity? R' (x) = (Use integers or decimals for any numbers in the expression.) What is the marginal revenue when x = 20? R' (20) = (Round to the nearest whole number as needed.)

Answer 1

The marginal revenue is

`(dR)/(dx)=(55ln(x)-55)/(ln(x)^2)`

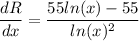
For x=20, the marginal revenue is R'=12.

Explanation:

The marginal revenue is defined as the additional revenue that yields an additional unit sale of the good.

Mathematically, is equivalent to the first derivative of the revenue function. In this case, we are not considering the additional cost, so we use the demand function.

The revenue then becomes

`R=p\cdot q=(55x)/(ln(x))`

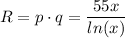
We can calculate this first derivative as:

`(dR)/(dx)=(d)/(dx)[55x/ln(x)] \\\\\\ u=55x\\\\v=ln(x)\\\\ (u/v)'=(u'v-uv')/v^2=(55ln(x)-55x/x)/ln(x)^2 \\\\(u/v)'=(55ln(x)-55)/ln(x)^2 \\\\\\(dR)/(dx)=(55ln(x)-55)/(ln(x)^2)`

The marginal revenue for x=20 is:

`(dR)/(dx)(20)=(55ln(20)-55)/(ln(20)^2)\\\\\\ (dR)/(dx)(20)=(55(3)-55)/(3^2)=(110)/(9)= 12.22\approx 12`