Question

The manager of an automobile dealership is considering a new bonus plan designed to increase sales volume. Currently, the mean sales volume is 14 automobiles per month. The manager wants to conduct a research study to see whether the new bonus plan increases sales volume. To collect data on the plan, a sample of sales personnel will be allowed to sell under the new bonus plan for a one-month period. a. Develop the null and alternative hypotheses most appropriate for this situation. b. Comment on the conclusion when H0 cannot be rejected. c. Comment on the conclusion when can be rejected. mean.

Answer 1

Null Hypothesis,
`H_0` :
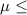`\mu \leq` 14 automobiles per month

Alternate Hypothesis,
`H_a` :
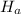`\mu` > 14 automobiles per month

Explanation:

We are given that the manager of an automobile dealership is considering a new bonus plan designed to increase sales volume. Currently, the mean sales volume is 14 automobiles per month.

The manager wants to conduct a research study to see whether the new bonus plan increases sales volume.

Let
`\mu` = population mean sales volume after the new bonus plan

So, Null Hypothesis,
`H_0` :
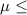`\mu \leq` 14 automobiles per month

Alternate Hypothesis,
`H_a` :
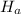`\mu` > 14 automobiles per month

Here, null hypothesis states that the new bonus plan does not increase the sales volume as the sales is less than or equal to 14 automobiles per month.

And alternate hypothesis states that the new bonus plan increases the sales volume as the sales is more than 14 automobiles per month.

Now, conclusion on when the null hypothesis (
`H_0`) can be rejected and when it cannot be rejected is based on two perspectives;

1. From test statistics point of view;

• If the test statistics is more than the critical value of any respective distribution, then we will reject our null hypothesis.

• If the test statistics is less than the critical value of any respective distribution, then we cannot reject our null hypothesis.

2. From P-value point of view;

• If the p-value of the test statistics is more than level of significance (
  `\alpha`), then we will not reject our null hypothesis.

• If the p-value of the test statistics is less than level of significance (
  `\alpha`), then we will reject our null hypothesis.