Question

The pupil of the eye is the circular opening through which light enters. its diameter can vary from about 8.00 mm to about 2.00 mm to control the intensity of the light reaching the interior. calculate the angular resolution, θr, of the eye for light that has a wavelength of 558 nm in both bright light and dim light.

Answer 1

The angular resolution is 0.0146°

Step-by-step explanation:

Given:

Diameter of pupil eye
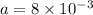`a = 8 * 10^(-3)` m

Diameter of pupil eye
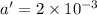`a' = 2 * 10^(-3)` m

Wavelength of light
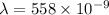`\lambda = 558 * 10^(-9)` m

According to rayleigh criterion,

`\sin \theta = 1.22 (\lambda)/(a)`

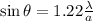
Where
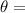`\theta =` angular resolution,
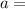`a =` diameter of aperture,

For larger diameter
`a`,

`\sin \theta _(1) = 1.22 (558 * 10^(-9) )/(8 * 10^(-3) )`

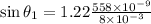
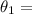`\theta _(1) =` 0.0049°

For smaller diameter
`a'`,

`\sin \theta _(2) = 1.22 (558 * 10^(-9) )/(2 * 10^(-3) )`

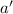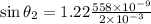
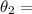`\theta _(2) =` 0.0195°

For finding the angular resolution,

`\theta _(r) = \theta _(2) - \theta _(1)`

`\theta _(r) = 0.0195 - 0.0049`

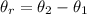
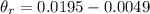
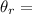`\theta _(r) =` 0.0146°

Therefore, the angular resolution is 0.0146°