Question

Assume a​ Cobb-Douglas production function of the​ form: q equals 10 Upper L Superscript 0.97 Baseline Upper K Superscript 0.18. What type of returns to scaleLOADING... does this production function​ exhibit? In this​ instance, returns to scale equal nothing. ​ (Enter a numeric response using a real number rounded to two decimal​ places.) This production function exhibits A. decreasing returns to scale. B. constant returns to scale. C. initially increasing but then constant returns to scale. D. initially constant but then increasing returns to scale. E. increasing returns to scale.

Answer 1

Returns to scale = 1.15

Increasing returns to scale.

Step-by-step explanation:

Cobb-Douglas production function of the​ form:

`q=10(L)^(0.97)(K)^(0.18)`

Here, we are using a simple rule of factors to find the returns to scale:

`q=10(tL)^(0.97)(tK)^(0.18)`

`q=10(t)^(0.97+0.18) (L)^(0.97)(K)^(0.18)`

`q=10(t)^(1.15) (L)^(0.97)(K)^(0.18)`

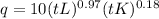
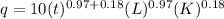
Hence,

By adding up the powers of L and K, we can get the returns to scale.

Returns to scale = 1.15

Suppose, the power of L be 'a' and the power of K is 'b',

if a + b = 1, then it exhibits constant returns to scale

if a + b > 1, then it exhibits increasing returns to scale

if a + b < 1, then it exhibits decreasing returns to scale.

In our case,

a + b = 1.15 which is greater than 1, so this production function exhibits increasing returns to scale.