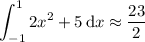Question

Integral from negative 1 to 1 left parenthesis 2 x squared plus 5 right parenthesis dxI. Using the trapezoidal rulea. Estimate the integral with nequals4 steps and find an upper bound for StartAbsoluteValue Upper E Subscript Upper T EndAbsoluteValue.Tequalsnothing​(Type an exact answer. Type an integer or a simplified​fraction.)An upper bound for StartAbsoluteValue Upper E Subscript Upper T EndAbsoluteValue isnothing.

Answer 1

Split the integration interval [-1, 1] into 4 subintervals:

[-1, -1/2], [-1/2, 0], [0, 1/2], [1/2, 1]

Each subinterval has a length of 1/2, which acts as the height of the corresponding trapezoid over the subinterval. The "bases" of the trapezoid are the function's values at the endpoint of the subinterval. For instance, over the first subinterval, we have

`f(x)=2x^2+5\implies\begin{cases}f(-1)=7\\f\left(-\frac12\right)=\frac{11}2\end{cases}`

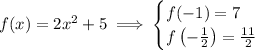
So over this subinterval, the trapezoid contributes an area of

`\frac{f(-1)+f\left(-\frac12\right)}2\cdot\frac12=\frac{25}8`

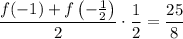
Do the same with the other 3 trapezoids; you'll find

`\displaystyle\int_(-1)^12x^2+5\,\mathrm dx\approx\frac{23}2`