Find a value of c so that y = x^2 - 12x + c has exactly one zero. A zero is an x-intercept. Find an equation with one x-intercept.

Question

asked Aug 5, 2021 19.0k views

1 Answer

Ben Thomson · Answer 1 · 2021-08-11T23:59:45+0000

Answer:

c=36

y = x^2 - 12x + 36

Explanation:

Given the equation
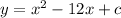
y = x^2 - 12x + c

We are to determine the value of c for which y has only one zero.

For the general form of a quadratic equation
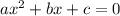ax^2+bx+c=0 , we can use the Discriminant to determine the nature of the roots.

If the Discriminant,
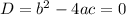D=b^2-4ac=0 , then the equation has equal roots, i.e. one x-intercept.

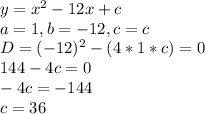
$y = x^2 - 12x + c\\a=1, b=-12, c=c\\D=(-12)^2-(4*1*c)=0\\144-4c=0\\-4c=-144\\c=36$

When c=36, the equation has only one root.

The equation therefore is:
y = x^2 - 12x + 36