Answer:
The value of the angle is
![\bf{ \sin^(-1)[h/am_(e)v]}](https://img.qammunity.org/2021/formulas/physics/high-school/119ue6sgoggvkgm4yn3pfj8q1jibqqfvcz.png) .
.
Step-by-step explanation:
Given:
The condition for diffraction minima is

where,
 is the slit-width,
is the slit-width,
 is the angle of incidence,
is the angle of incidence,
 is the order number and
is the order number and
 is the wavelength of the light.
is the wavelength of the light.
The wavelength of an electron traveling through a medium is governed by de Broglie's hypothesis.
According to de Broglie's hypothesis

Here,
 is Planck's constant,
is Planck's constant,
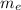 is the mass of the electron and
is the mass of the electron and
 is the velocity of the electron.
is the velocity of the electron.
For first minimum
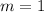 .
.
From equation (1), we have
![&& a \sin \theta = (h)/(m_(e)v)\\&or,& \theta = \sin^(-1)[(h)/(am_(e)v)]](https://img.qammunity.org/2021/formulas/physics/high-school/gf36exh2zyzd72rztmx78qs27ok8br9ibi.png)