Question

A block of mass m is attached to a rope wound around the outer rim of a disk of radius R and moment of inertia I, which is free to rotate around an axle passing through its center of mass. The rope does not slip. What are the acceleration of the block and the tension in the string

Answer 1

Step-by-step explanation:

I is the moment of inertia of the pulley, α is the angular acceleration of the pulley and T is the tension in the rope. Let a is the linear acceleration.

The relation between the linear acceleration and the angular acceleration is

a = R α .... (1)

According to the diagram,

T x R = I x α

T x R = I x a / R from equation (1)

T = I x a / R² .... (2)

mg - T = ma .... (3)

Substitute the value of T from equation (2) in equation (3)

`mg - (Ia)/(R^(2))=ma`

`a=(mg)/(m+(I)/(R^(2)))`

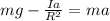
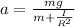
T is the acceleration in the system

Substitute the value of a in equation (2)

`T = (I)/(R^(2))* (mg)/(m+(I)/(R^(2)))`

`T=(I* mg)/(I+mR^(2))`

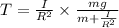
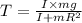
This is the tension in the string.