Question

Find the standard form of the circle x2 + y2 – 6x + 10y + 24 = 0 by completing the square.

Answer 1

`(x-3)^2+ (y+5)^2=10`

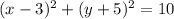
Explanation:

Given the equation of the circle:
`x^2 + y^2 - 6x + 10y + 24 = 0`

We wish to express it in a Standard form:

We begin by re-arranging:

`x^2 - 6x + y^2 + 10y = - 24`

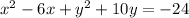
Next, divide the coefficient of x by 2, square it and add it to both sides.

Do the same for y.

`x^2 - 6x +(-3)^2+ y^2 + 10y+5^2 = - 24+(-3)^2+5^2`

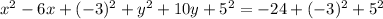
Next, we factorize

`(x-3)^2+ (y+5)^2 = - 24+9+25\\(x-3)^2+ (y+5)^2=10`

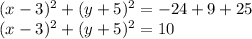
This is the standard form.