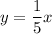Answer:
Option C)
Explanation:
We are given the following in the question:
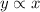
Removing the sign of proportionality and introducing the constant of proportionality, we have
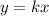
where k is constant of proportionality.
We are given
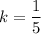
Putting value, we get,
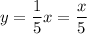
Thus, the equation representing the relationship is
Option C)