Question

Given the function f(x)=2x3−15x2 over the interval −1≤x≤6, answer the following questions. (a) Find f′(x) and f′′(x). f′(x)= f′′(x)= (b) Find the critical points of f. Enter the exact answers in increasing order. x1= x2= (c) Find any inflection points of f. Enter the exact answer.

Answer 1

Explanation:

Consider the function
`f(x) = 2x^3-15x^2` over the given interval.

a)Recall that the following derivatives' properties:

-
`(x^n)' = n x^(n-1)`

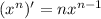
-(f+g)' = f'+g' when f and g are differentiable

-(cf)' = cf', where c is a constant and f a differentiable function.

Then, using this properties we have that

`f'(x) = 2\cdot 3 x^(2)- 15  \cdot 2 x = 6x^2-30x`

`f''(x) = 6\cdot 2 x -30 = 12x-30`

b) Recall that a critical point of a function f is where it's derivatives are 0 or they don't exist. From point a we have that both f' and f'' are polynomials, so the derivatives are continous. Hence,the critical points are where the first derivative is equal to zero.

Then, we have the following equation

`6x^2-30x = 0 = x(6x-30) = 6x(x-5)`

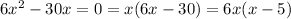
Hence, the only critical points are x=0 and x=5.

c) Recall that the inflection points are were f''(x) is zero. Then, we have the following equation

`12x-30=0`

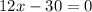
The solution of this equation is
`x=(30)/(12)= (5)/(2)=2.5`

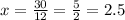
so x=2.5 is an inflection point of the function f