Answer:
The expression
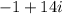 represents the number
represents the number
 rewritten in a+bi form.
rewritten in a+bi form.
Explanation:
The value of
 is
is
![i=√(-1)[tex] or [tex]i^(2)=-1[\tex].</strong></p><p>Now [tex]i^(4)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/krqxfho7lmemxf8n9uogizmwde43t9prew.png) in term of
in term of
![i^(2)[\tex] can be written as, </p><p>[tex]i^(4)=i^(2)* i^(2)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ba7jsbafk1r0460jcjic8dl70mvb5zrtkx.png)
Substituting the value,
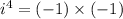
Product of two negative numbers is always positive.
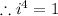
Now
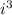 in term of
in term of
![i^(2)[\tex] can be written as, </p><p>[tex]i^(3)=i^(2)* i](https://img.qammunity.org/2021/formulas/mathematics/middle-school/c9cmnpfqdqs7wpea1a7qmexhxxw0bxnz9c.png)
Substituting the value,
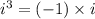
Product of one negative and one positive numbers is always negative.
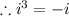
Now
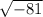 can be written as follows,
can be written as follows,
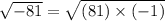
Applying radical multiplication rule,
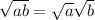
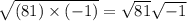
Now,
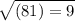 and
and
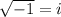
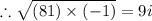
Now substituting the above values in given expression,
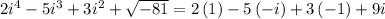
Simplifying,

Collecting similar terms,

Combining similar terms,
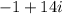
The above expression is in the form of a+bi which is the required expression.
Hence, option number 4 is correct.