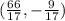Question

Gandalf the Grey started in the Forest of Mirkwood at a point PP with coordinates (2,−1)(2,−1) and arrived in the Iron Hills at the point QQ with coordinates (3, 3). If he began walking in the direction of the vector v=4i+1jv=4i+1j and changes direction only once, when he turns at a right angle, what are the coordinates of the point where he makes the turn?

Answer 1

`((66)/(17),-(9)/(17))`

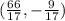
Explanation:

Gandalf's Starting Point is given as: P(2,-1)

If he walks in the direction of the vector v=4i+1j

x=4, y=1

The slope of the line which he walked therefore is:
`m_1=(1)/(4)`

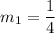
First, we determine the equation of the line at P with coordinates (2,-1)

`y-y_1=m(x-x_1)\\y-(-1)=(1)/(4)(x-2)\\ y+1=(1)/(4)x-(1)/(2)\\y=(1)/(4)x-(1)/(2)-1\\y=(1)/(4)x-(3)/(2)`

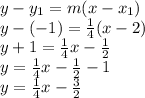
If he changes direction at a right angle, the new path walked is perpendicular to the old path.

DEFINITION: Two lines are perpendicular if the product of their gradients
`m_1m_2=-1`

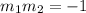
Therefore the gradient
`m_2` of the new path walked
`=-4`

At point Q with coordinates (3,3), the equation of the line is:

`y-y_1=m(x-x_1)\\y-3=-4(x-3)\\y=-4x+12+3\\y=-4x+15`

The coordinate where Gandalf the Grey makes a turn is the intersection of the two lines.

`If \: y=(1)/(4)x-(3)/(2) \:and\: y=-4x+15\\Then:\\(1)/(4)x-(3)/(2) =-4x+15\\(1)/(4)x+4x=15+(3)/(2)\\4.25x=16.5\\x=(66)/(17)\\y=-4x+15=-4((66)/(17))+15=-(9)/(17)`

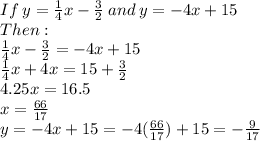
Therefore, the coordinates where he makes a turn is:

`((66)/(17),-(9)/(17))`