Question

A car travels at a steady 40.0 m/s around a horizontal curve of radius 200 m. What is the minimum coefficient of static friction between the road and the car's tires that will allow the car to travel at this speed without sliding?

A. 1.23B. 0.662C. 0.816D. 0.952E. 0.736

Answer 1

The minimum coefficient of static friction between the road and the car's tires is 0.816

Option "C"

Step-by-step explanation:

Given;

velocity of the car, v = 40.0 m/s

radius of horizontal curve, r = 200 m

For a minimum coefficient of static friction between the road and the car's tires that will allow the car to travel at the given speed without sliding, centripetal force must equal frictional force.

`F_(frictional) = F_(centripetal)\\\\\mu mg = (mv^2)/(r) \\\\\mu = (v^2)/(rg)`

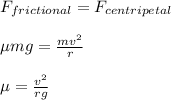
where;

μ is the minimum coefficient of static friction

`\mu = (40^2)/(200*9.8) \\\\\mu = 0.816`

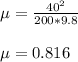
Thus, the minimum coefficient of static friction between the road and the car's tires is 0.816

Option "C"