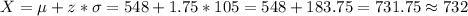Answer:
a) a=0.181912
b) The probability of getting a score of more than 500 is P=0.677
c) Minimum score to be admitted = 732
Explanation:
a) The cutoff value a can be looked-up from a standard normal distribution table or applet.
The value for a to have P(Z<a)=0.575 is a=0.18912.
b) To calculate the probability of a value in a not-standard normal distribution, we can transform it to the standard form and look up for the value of the z-score.
If the distribution has a mean of 548 and a standard deviation of 105, the probabilty o getting a score of more than 500 is:
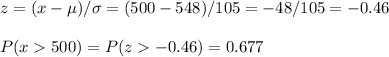
The probability of getting a score of more than 500 is P=0.677.
c) Scoring more than the 96th percentile means that only will be admitted if the score is higher than the 96% of the population of scores.
As it is a normal distribution, we first calculate the z-score for which 96% of the values lies below:

Then, we convert this z-score to the score distribution as: