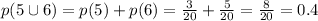Answer:
0.4
Explanation:
These are the relative frequencies of each face (data are missing in the text of the problem):
Number Showing on Top Face Frequency
1 0
2 3
3 3
4 6
5 3
6 5
The probability to obtain a certain number when throwing the dice is given by
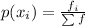
where
 is the relative frequency of the number
is the relative frequency of the number
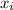 to occur
to occur
 is the sum of the relative frequencies
is the sum of the relative frequencies
Here the sum of the frequencies is:
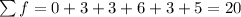
For number 5 here, we have:
 (from the table)
(from the table)
So the probability of getting a 5 is
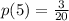
For number 6 here, we have
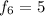
So the probability of getting a 6 is
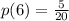
So the probability to obtain either a 5 or a 6 in the next rolling is: