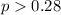Answer:
In order to apply the z proportion test we need to verify the following conditions:
1) Randomization we need a random sample.
2) 10 % condition we need that the sample size would be lower than 10% of the population size
3) We need to satisfy the normalyti condition:
n⋅p≥10 and n⋅(1−p)≥10
And for this case we satisfy all the conditions
We need to conduct a hypothesis in order to test the claim that the true proportion is higher than 0.28, so the correct system of hypothesis are:
Null hypothesis:
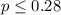
Alternative hypothesis:
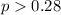
Step-by-step explanation:
Data given and notation
n=141 represent the random sample taken
X=43 represent the adults that were infected with Lyme disease
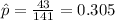 estimated proportion of adults infected with Lyme disease
estimated proportion of adults infected with Lyme disease
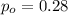 is the value that we want to test
is the value that we want to test
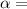 represent the significance level
represent the significance level
z would represent the statistic (variable of interest)
 represent the p value (variable of interest)
represent the p value (variable of interest)
Solution to the problem
In order to apply the z proportion test we need to verify the following conditions:
1) Randomization we need a random sample.
2) 10 % condition we need that the sample size would be lower than 10% of the population size
3) We need to satisfy the normalyti condition:
n⋅p≥10 and n⋅(1−p)≥10
And for this case we satisfy all the conditions
We need to conduct a hypothesis in order to test the claim that the true proportion is higher than 0.28, so the correct system of hypothesis are:
Null hypothesis:
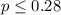
Alternative hypothesis: