Question

Assume that the speed of light in a vacuum has the hypothetical value of 18.0 m/s. A car is moving at a constant speed of 14.0 m/s along a straight road. A home owner sitting on his porch sees the car pass between two telephone poles in 8.89 s. How much time does the driver of the car measure for his trip between the poles?

Answer 1

Observed time, t = 5.58 s

Step-by-step explanation:

Given that,

Speed of light in a vacuum has the hypothetical value of, c = 18 m/s

Speed of car, v = 14 m/s along a straight road.

A home owner sitting on his porch sees the car pass between two telephone poles in 8.89 s.

We need to find the time the driver of the car measure for his trip between the poles. The relation between real and observed time is given by :

`T=\frac{t}{\sqrt{1-(v^2)/(c^2)} }`

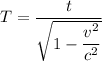
t is observed time.

`t=T* \sqrt{1-(v^2)/(c^2)} \\\\t=8.89* \sqrt{1-(14^2)/(18^2)} \\\\t=5.58\ s`

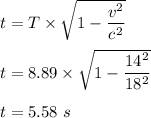
So, the time observed by the driver of the car measure for his trip between the poles is 5.58 seconds.