Question

If AE=6x-55 and EC=3x-16, find DB. (Hint: Find x first and then substitute.)

Answer 1

Given:

Given that ABCD is a rectangle.

The diagonals of the rectangle are AC and DB.

The length of AE is (6x -55)

The length of EC is (3x - 16)

We need to determine the length of the diagonal DB.

Value of x:

The value of x can be determined by equating AE and EC

Thus, we have;

`AE=EC`

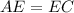
Substituting the values, we get;

`6x-55=3x-16`

`3x-55=-16`

`3x=39`

`x=13`

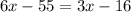
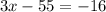
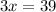
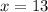
Thus, the value of x is 13.

Length of AC:

Length of AE =
`6(13)-55=78-55=23`

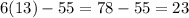
Length of EC =
`3(13)-16=39-16=23`

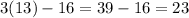
Thus, the length of AC can be determined by adding the lengths of AE and EC.

Thus, we have;

`AC=AE+EC`

`AC=23+23`

`AC=46`

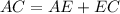
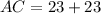
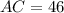
Thus, the length of AC is 46.

Length of DB:

Since, the diagonals AC and DB are perpendicular to each other, then their lengths are congruent.

Hence, we have;

`AC=DB`

`46=DB`

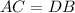
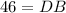
Thus, the length of DB is 46.