Question

An elastic circular conducting loop expands at a constant rate in time. The radius is initially 0.200 m. but then begins to increase 0.018 m every second. The loop has a constant resistance of 15 Ohm and Is placed in a region of uniform (same everywhere) magnetic field of 0.880 T, perpendicular to the plane of the loop. Calculate the magnitude of the Induced curt 2.4 s after the loop begins expanding.

Answer 1

The magnitude of the induced current is 1.6 mA

Step-by-step explanation:

The induced emf in the loop is:

`E=-(d\phi )/(dt)\\ E=-2\pi r(t)B*0.018`

`r(t)=r_(o) +0.018t=0.2+0.018t`

t = 2.4 s

`r(t)=0.2+(0.018*2.4)=0.243m`

`E=-2\pi *0.243*0.88*0.018=-0.024V=-24mV`

The induced current is:

`I=(E)/(R) =(24)/(15) =1.6mA`

Answer 2

4.5 mA

Step-by-step explanation:

Parameters given:

Initial radius of coil = 0.2 m

Rate of expansion of coil = 0.018 m/s

Resistance, R = 15 ohms

Magnetic field, B = 0.88 T

Time taken to expand, t = 2.4 s

To find the induced current, we have to first find the induced EMF. This can be gotten by using the formula below:

`V = (-BA)/(t)`

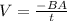
where A = area of coil

To find the area, we need to find the radius of the coil 2.4 seconds after it started expanding.

After 2.4s, the coil had expanded to become:

r = 0.2 + (0.018 * 2.4) = 0.2 + 0.0432 = 0.2432 m

Area =
`\pi r^2` =
`\pi * 0.2432^2 = 0.186 m^2`

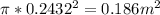
The magnitude of the Voltage induced will be:

`|V| = |(-0.88 * 0.186)/(2.4)| \\\\\\|V| = 0.068 V`

From Ohm's law, we have that:

`|V| = |I|R`

=>
`|I| = (|V|)/(R)`

`|I| = (0.068)/(15)`

`|I| = 0.0045 A = 4.5 mA`

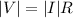
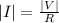
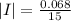
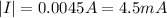
The magnitude of the Induced curt 2.4 s after the loop begins expanding is 4.5 mA