Question

An optical disk drive in your computer can spin a disk up to 10,000 rpm (about 1045 rad/s 1045 rad/s ). If a particular disk is spun at 968.7 rad/s 968.7 rad/s while it is being read, and then is allowed to come to rest over 0.234 seconds 0.234 seconds , what is the magnitude of the average angular acceleration of the disk?

Answer 1

The magnitude of the average angular acceleration of the disk is
`4139.74\ rad/s^2`.

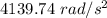Step-by-step explanation:

Given that,

Angular velocity,
`\omega_i=968.7\ rad/s`

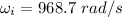
The disk comes to rest,
`\omega_i=0`

Time, t = 0.234 s

We need to find the magnitude of the average angular acceleration of the disk. It is given by change in angular velocity per unit time. So,

`\alpha =(\omega f)/(t)\\\\\alpha =(968.7\ rad/s)/(0.234\ s)\\\\\alpha =4139.74\ rad/s^2`

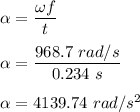
So, the magnitude of the average angular acceleration of the disk is
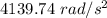`4139.74\ rad/s^2`.