Question

Xcel energy uses the equation c (x) =7.1+23logx to determine the cost of electricity for x hours. A. What would the function c^-1(x) allow you to calculate. B. Find c^-1(x). C. If a customer can afford $15 per month for electricity, how long can he or she have electricity turned on?

Answer 1

Please read the answer below

Explanation:

We have the function

`y(x)=7.1+23logx`

A. With c^{-1}(x) we can calculate the hours of electricity for a definite cost

B.

c^{-1} can be calculated by taking into account that:

`c^(-1)(x)=(1)/(c(x))=(1)/(7.1+23logx)`

the denominator must be different of zero, hence we have for x:

`7.1+23logx=0\\\\7.1+logx^(23)=0\\\\logx^(23)=-7.1\\\\10^{logx^(23)}=10^(-7.1)\\\\x^23=10^(-7.1)\\\\x=10^{(-7.1)/(23)}=0.49\approx0.5`

x must be different of 0.48

C.

By taking apart the function c(x) we have:

`logx^(23)=15-7.1=7.9\\\\10^{logx^(23)}=10^(7.9)\\\\x=10^{(7.9)/(23)}=2.2h`

x=2.2h

hope this helps!

Answer 2

Explanation:

Note that the cost function is
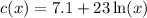`c(x) = 7.1+23\ln(x)`, which gives us the cost of electricity for x hours of consumption

a). The function

To find out the inverse function, we interchange the labels of x and y and solve for y, that is

`x = 7.1+23\ln(y)`

when solved for y we have

`e^{(x-7.1)/(23)}= y`

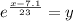
So the inverse function is given by
`c^(-1)(x) = e^{(x-7.1)/(23)}`.

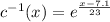c) We will use the inverse function to find the amount of hours the customer can use eelectricity. It is simple obtained by evaluating the inverse function at the desired cost (i.e
`c^(-1)(15)`)

that is

`e^{(15-7.1)/(23)} = 1.409`

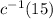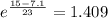
that is, the custome can consume at most 1.41 hours of electricity.