Answer:
− 3 y ' ' − 3 y ' + 3 y = 0 : over-damped
− 2 y ' ' − 4 y ' + 1 y = 0 : over-damped
1 y ' ' + 7 y ' + 5 y = 0: over-damped
Explanation:
Using the characteristic equation you can express a differential equation of order n as an algebraic equation of degree n:
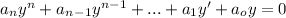
This differential equation will have a characteristic equation of the form:

Now, you can classify the solution for a differential equation using a simple method. In order to do it, you just need to use the discriminant.
- If the discriminant is greater than zero, the solution is over-damped
- If the discriminant is less than zero, the solution is under-damped
- If the discriminant is equal to zero, the solution is critically damped
So, given the differential equation:
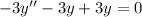
Which has characteristic equation of the form:
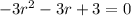
The quadratic polynomial of the form:
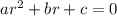
Has discriminant:
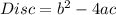
In this case:

So:
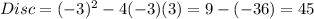
In this case:
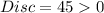
Therefore the solution is over-damped.
Now, given the differential equation:
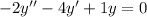
Which has characteristic equation of the form:
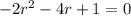
The quadratic polynomial of the form:
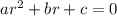
Has discriminant:
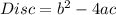
In this case:
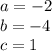
So:
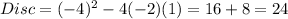
In this case:
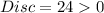
Therefore the solution is over-damped.
Finally, given the differential equation:
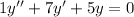
Which has characteristic equation of the form:

The quadratic polynomial of the form:
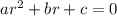
Has discriminant:
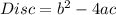
In this case:
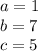
So:
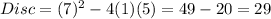
In this case:
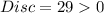
Therefore the solution is over-damped.