Answer:
Third option.
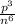
Explanation:
For this exercise you need to remember one of the properties for exponents.
There is a property called the "Negative property of exponents" which states the following:
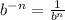
Where

As you can observe,
 is the reciprocal of
is the reciprocal of
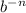
In this case you have the following expression given in the exercise:

Observe the expression. As you can notice, the base "n" has a negative exponent, which is -6.
Therefore, applying the Negative property of exponents explained at the beginning of this explanation, you can simplify the expression.
Then, the simplified form of
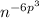 is the one shown below:
is the one shown below:
