Question

1. How many ways are there to make an octagon with 19 different sticks when order doesn’t matter?

2. How many ways are there to make an octagon with 19 different sticks when order matters?

Answer 1

1. 75,582 ways

2. 3,047,466,240 ways

Explanation:

1-An octagon is an 8-sided polygon.

-A combination is an arrangement of a sequence without any defined order. Order doesn't matter

-Given that there are 19 sticks, the combination to form octagons can be calculated as:

`(\limits^n_k)=(n!)/(k!(n-k)!)\\\\(\limits^(19)_8)=(19!)/(8!(19-8)!)\\\\=75,582\ ways`

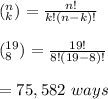
Hence, there are 75,582 ways to arrange the sequence in nor particular order.

2. This question tests our knowledge of permutations.

-A permutation is an arrangement of a set's elements in a defined order.

-Permutation is given by the formula:

`P(n,r)=(n!)/((n-r)!), \ \ \ n=19, r=8\\\\P(19,8)=(19!)/((19-8)!)\\\\=3047466240 \ \ ways`

Hence, there are 3,047,466,240 ways to make an octagon from 19 sticks in an ordered manner.