Question

A velodrome is built for use in the Olympics. The radius of curvature of the surface is 20.0 m. At what angle should the surface be banked for cyclists moving at 22.0 m/s? (Choose an angle so that no frictional force is needed to keep the cyclists in their circular path. Large banking angles are used in velodromes.)

Answer 1

The angle of baking for the cyclist is 67.54 degrees.

Step-by-step explanation:

Given that,

Radius of curvature of the surface, r = 20 m

Speed of the cyclist, v = 22 m/s

We need to find the angle of banking for the cyclists. In this type of motion, the centripetal force is balanced by the frictional force between vehicle and the cyclist such that we get the angle of banking as :

`\tan\theta=(v^2)/(rg)\\\\\theta=\tan^(-1)((v^2)/(rg))\\\\\theta=\tan^(-1)(((22)^2)/(20* 10))\\\\\theta=67.54^(\circ)`

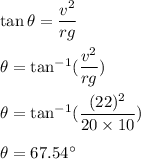
So, the angle of baking for the cyclist is 67.54 degrees.