Question

Your company produces electrical components for a government project that are normally distributed with a mean frequency of 100 MHz and a variance of 9 MHz. The government accepts product that falls between 95.06 MHz and 105.88 MHz. What percent of our product will be acceptable to the government? Note that

a. 68.00%
b. 95.00%
c. 92.50%
d. 97.20%
e. 90.00%

Answer 1

Option C) 92.50%

Explanation:

We are given the following information in the question:

Mean, μ = 100 MHz

Variance = 9 MHz

`\sigma^2 = 9\\\sigma = 3`

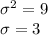
We are given that the distribution of frequency is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

P( product that falls between 95.06 MHz and 105.88 MHz)

`P(95.06 \leq x \leq 105.88)\\\\ = P(\displaystyle(95.06 - 100)/(3) \leq z \leq \displaystyle(105.88-100)/(3))\\\\ = P(-1.645 \leq z \leq 1.96)\\\\= P(z \leq 1.96) - P(z < -1.645)\\= 0.975 - 0.05 =0.925 = 92.5\%`

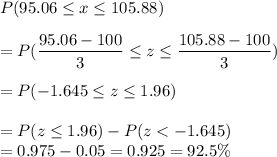
92.5% of product will be acceptable to the government.

Thus, the correct answer is

Option C) 92.50%