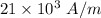Question

A toroid filled with a magnetic substance carries a steady current of 2.95 A. The coil contains 1430 turns, has an average radius of 3.14 cm. The magnetic field through the toroid is 0.0659686 T. Assume the flux density is constant. What is the magnetic field strength H within the core in the absence of the magnetic substance?

Answer 1

Magnetic field strength,
`H=21* 10^3\ A/m`

Step-by-step explanation:

Given that,

Current in the toroid, i = 2.95 A

Number of turns in the toroid, N = 1430

Radius of the toroid, r = 3.14 cm

The magnetic field through the toroid is 0.0659686 T.

We need to find the magnetic field strength H within the core in the absence of the magnetic substance. The relation between magnetic field and the magnetic field strength is given by :

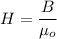`H=(B)/(\mu_o)` .........(1)

B is external magnetic field

The magnetic field for the toroid is given by :

`B=(\mu_oi N)/(2\pi r)\\\\B=(4\pi * 10^(-7)* 1430* 2.95)/(2\pi * 3.14* 10^(-2))\\\\B=0.0268\ T`

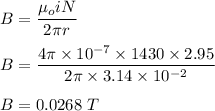
Equation (1) becomes :

`H=(0.0268)/(4\pi * 10^(-7))\\\\H=21326.76\ A/m\\\\H=21* 10^3\ A/m`

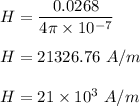
So, the magnetic field strength H within the core in the absence of the magnetic substance is
`21* 10^3\ A/m`