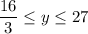Question

Mousio asked Feb 23, 2023

377,617 views

2 Answers

Execjosh · Answer 1 · 2023-02-26T09:33:14+0000

Answer:

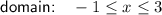
$\textsf{domain:}\quad-1\leq x\leq 3$

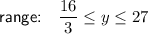
$\textsf{range:}\quad(16)/(3)\leq y\leq 27$

Explanation:

Information

Domain of a function: set of all possible input values (x-values)

Range of a function: set of all possible output values (y-values)

Closed circle: less than or equal to and greater than or equal to (≤ or ≥).

Open circle: less than or greater than (< or >)

Domain

There is a closed dot at x = -1 and x = 3

Therefore, the domain is -1 ≤ x ≤ 3

Range

To calculate the exact range, we need to figure out the equation of the function (as it is difficult to read the exact value of y at x = -1).

From inspection of the graph, we can identify the following ordered pairs:

(1, 12) (2, 18) (3, 27)

General form of an exponential equation:
y=ab^x

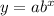
Inputting the first two ordered pairs into the exponential equation:

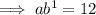
$\implies ab^1=12$

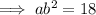
$\implies ab^2=18$

Dividing the equations to find b:

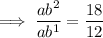
$\implies (ab^2)/(ab^1)=(18)/(12)$

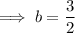
$\implies b=\frac32$

Inputting b into the first equation to find a:

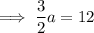
$\implies \frac32a=12$

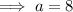
$\implies a=8$

Therefore, the equation of the function is:
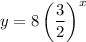
$y=8\left(\frac32\right)^x$

Input
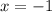x = -1 into the equation to find y:

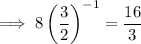
$\implies 8\left(\frac32\right)^(-1)=(16)/(3)$

Therefore, the range is
$(16)/(3)\leq y\leq 27$

Your comment on this question: