Question

When the production function is​ linear: q​ = 0.25L​ + 0.75K, the factors are perfect substitutes for one another and the isoquant is linear. Determine the equation for the isoquant when output equals 20 units. A. Upper K equals 26.67 minus 0.333 Upper L B. Upper K equals 33.33 minus 0.267 Upper L C. Upper K equals 26.67 plus 0.333 Upper L Assuming capital is plotted on the vertical axis and labor is plotted on the horizontal​ axis, what is the marginal rate of technical substitution in this​ case? MRTS​ = nothing ​(Round your answer to two decimal​ places.)

Answer 1

Option (A) is correct.

MRTS(L,K) = -0.33

Step-by-step explanation:

Given that,

Linear production function: q​ = 0.25L​ + 0.75K

(a) The equation for isoquant is calculated as follows:

At output level of 20 units,

q​ = 0.25L​ + 0.75K

20 = 0.25L + 0.75K

0.75K = 20 - 0.25L

K = 26.67 - 0.33L

(b) Assuming capital is plotted on the vertical axis and labor is plotted on the horizontal​ axis,

The marginal rate of technical substitution is indicating the relationship between the level of inputs used and trade offs, where the level of output remains constant.

Here, the MRTS is given as the rate of change of factor K upon the rate of change of factor L.

Therefore, it is simply calculated by differentiating the above isoquant equation,

`(dK)/(dL)=0-0.33`

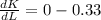
= -0.33