Question

In some proton accelerators, proton beams are directed toward each other for head-on collisions. Suppose that in such an accelerator, protons move with a speed relative to the lab of 0.9898c.

(a) Calculate the speed of approach of one proton with respect to another one with which it is about to collide head on. Answer given for is .99995c.

(b) What is the kinetic energy of each proton (in units of MeV) in the laboratory reference frame? Answer given is 5640MeV.

(c) What is the kinetic energy of one of the colliding protons (in units of MeV) in the rest frame of the other proton? Answer given is 91500MeV.

Answer 1

a) 0.9995c

b) 5641MeV

c) 91670 MeV

Step-by-step explanation:

(a) The speed of approach is given by the formula:

`u=(v_1+v_2)/(1+(v_1v_2)/(c))=(2(0.9898c))/(1+((0.9898)^2c^2)/(c^2))=0.99995c`

(b) the kinetic energy is given by:

`E_k=m_0c^2[\frac{1}{\sqrt{1-(v^2)/(c^2)}}-1]`

by replacing c=3*10^8m/s, m_0=1.67*10^{-27}kg we obtain:

`E_k=5641MeV`

(c) in the rest frame of the other proton we have:

`E_k=m_0c^2[\frac{1}{\sqrt{1-(u^2)/(c^2)}}-1]`

by replacing we get

`E_k=91670MeV`

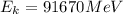
hope this helps!!