Answer:
Option C) 5.62 points
Explanation:
We are given the following in the question:
Sample size, n = 20
Sample mean score = 64
Sample standard deviation, s = 12
Degree of freedom =
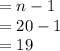
We have to calculate margin of error for a 95% confidence interval.
Formula for margin of error:
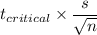
Putting the values, we get,
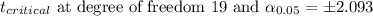
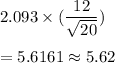
Thus, the correct answer is
Option C) 5.62 points