Answer:
see the answers below please
Step-by-step explanation:
We have that the current in the inner solenoid is:
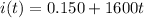
A) the magnetic flux is given by
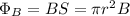
B is obtained by computing for a solenoid:
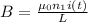
hence, we have
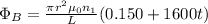
B)
the mutual inductance is obtained by using:
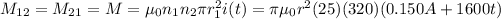
C)
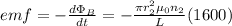
hope this helps!!