Question

A random sample of 121 checking accounts at a bank showed an average daily balance of $280. The standard deviation of the population is known to be $66. It will still be necessary to know something about the shape of the distribution of the account balances in order to make an interval estimate of the mean of all the account balances. False True

Answer 1

False

Explanation:

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

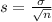For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

In this problem

Sample of 121, which is higher than 30.

So we do not need to know anything about the shape of the distribution in order to make an interval estimate of the mean of all the account balances.

So the answer is False