Question

A savings and loan association needs information concerning the checking account balances of its local customers. A random sample of 14 accounts was checked and yielded a mean balance of $664.14 and a standard deviation of $297.29.

a) Find a 98% confidence interval for the true mean checking account balance for local customers.
b) Find a 95% confidence interval for the standard deviation.

Answer 1

a) 98% confidence interval for the true mean checking account balance for local customers.

(453.586 , 874.693)

b) 95% confidence interval for the standard deviation.

(214.91 , 441.53)

Explanation:

Given a size of sample 'n' =14

given mean of the sample x⁻ = $664.14

standard deviation of the sample 'S' = $297.29.

a)

98% of confidence intervals

`(x^(-) - t_(\alpha ) (S)/(√(n) ) , x^(-)+ t_(\alpha )(S)/(√(n) ) )`

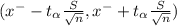
The degrees of freedom γ=n-1 =14-1 =13

t₁₃ = 2.650 at 98% of confidence level of signification.

`(664.14- 2.650(297.29)/(√(14) ) , 664.14+ 2.650(297.29)/(√(14) ) )`

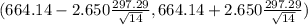
on calculation, we get

(664.14-210.553 , 664.14+210.553)

(453.586 , 874.693)

98% confidence interval for the true mean checking account balance for local customers.

(453.586 , 874.693)

95% of confidence intervals

`({s\sqrt{\frac{n-1}{X^(2) _{((\alpha )/(2) ,n-1) } } } ,s\sqrt{\frac{n-1}{X^2_{(1-\alpha )/(2),n-1 } } } )`

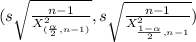
The degrees of freedom γ=n-1 =14-1 =13

X^2_{0.05,13} =22.36 (check table)

X^2_{0.95,13} = 5.892 (check table)

`(297.29. (\sqrt{(14-1)/(X^2_(0.05,13) ) } ),297.29(\sqrt{(14-1)/(X^2_(0.95,13) ) } )`

`(297.29. (\sqrt{(14-1)/(22.36 ) } ),297.29(\sqrt{(14-1)/(5.892 ) } )`

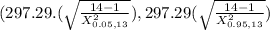
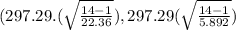
(214.91 , 441.53)

95% confidence interval for the standard deviation.

(214.91 , 441.53)