Answer:
a) 98% confidence interval for the true mean checking account balance for local customers.
(453.586 , 874.693)
b) 95% confidence interval for the standard deviation.
(214.91 , 441.53)
Explanation:
Given a size of sample 'n' =14
given mean of the sample x⁻ = $664.14
standard deviation of the sample 'S' = $297.29.
a)
98% of confidence intervals
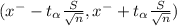
The degrees of freedom γ=n-1 =14-1 =13
t₁₃ = 2.650 at 98% of confidence level of signification.
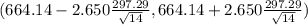
on calculation, we get
(664.14-210.553 , 664.14+210.553)
(453.586 , 874.693)
98% confidence interval for the true mean checking account balance for local customers.
(453.586 , 874.693)
95% of confidence intervals
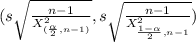
The degrees of freedom γ=n-1 =14-1 =13
X^2_{0.05,13} =22.36 (check table)
X^2_{0.95,13} = 5.892 (check table)
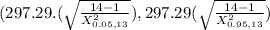
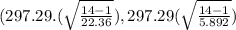
(214.91 , 441.53)
95% confidence interval for the standard deviation.
(214.91 , 441.53)