Question

A frozen dinner is divided into 3 sections on a circular plate with a 12-inch diameter. The central angle formed by the peach cobbler is 105 degrees. The central angle formed by the pasta is 203 degrees. What is the approximate length of the arc of the section containing the peas? A. 3 inches B. 21 inches C. 16 inches D. 5 inches

Answer 1

D. 5 inches

Explanation:

Given:

A frozen dinner is divided into 3 sections on a circular plate with a 12-inch diameter.

That means complete angle having 360° is divided into 3 section.

The central angle formed by the peach cobbler is 105 degrees.

The central angle formed by the pasta is 203 degrees.

Question asked:

What is the approximate length of the arc of the section containing the peas?

Solution:

The central angle formed by the peas = 360° - 105° - 203°

= 52°

`Ridius,r=(Dameter)/(2) =(12)/(2) =6\ inches`

As we know:

`Length\ of\ arc=2\pi r*(\Theta )/(360)`

`=2*(22)/(7) *6*(52)/(360) \\ \\ =(13728)/(2520) \\ \\ =5.44\ inches`

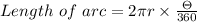
Therefore, the approximate length of the arc of the section containing the peas are 5 inches.