Question

A population of 2000 starfish has a yearly per capita population growth rate of 0.012. By next year, how do you expect population size to have changed?

Assume that the population grows exponentially according to the equation d N d t = r N

It will increase by 50 starfish
It will increase by 24 starfish
It will increase by 100 starfish
It will increase by 200 starfish

Answer 1

It will increase by 24 starfish

Explanation:

The population is modeled by the following differential equation:

`(dN)/(dt) = rN`

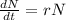
Which has the following solution:

`N(t) = N(0)e^(rt)`

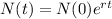
In which N(0) is the initial population and r is the growth rate.

A population of 2000 starfish has a yearly per capita population growth rate of 0.012.

This means that
`N(0) = 2000, r = 0.012`

By next year, how do you expect population size to have changed?

This is N(1).

`N(t) = N(0)e^(rt)`

`N(1) = 2000*e^(0.012)`

`N(1) = 2024`

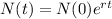
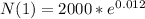
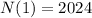
2024 - 2000 = 24

So the correct answer is:

It will increase by 24 starfish