Answer:
Her speed at the bottom of the slope is 25.665 m/s
Step-by-step explanation:
Here we have
Initial velocity, v₁= 15 m/s
Final velocity = v₂
The energy balance present in the system can be represented as

Where:
m = Mass of the cyclist = 70 kg
W = work done by the drag force =
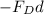
Where:
d = Distance traveled = 450 m
Therefore,
 and
and
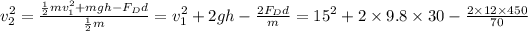
= 658.714 m²/s²
v₂ = 25.665 m/s
Her speed at the bottom of the slope = 25.665 m/s.