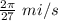Answer:
the velocity of the missile when the angle of elevation from the tracking station is 30 degrees =
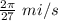
Step-by-step explanation:
The method employed in solving this question is to relate it to a right- angled triangle;
Now ; if we consider the missle fired vertically from a point 5 miles from tracking station ; with an angle θ and h becoming the height :
Then ;
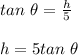
Differentiating the above equation ; we have
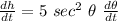
Replacing
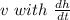 ;
;
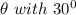 and
and
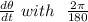 ; we have :
; we have :
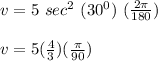
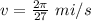
Thus,the velocity of the missile when the angle of elevation from the tracking station is 30 degrees =