Question

A 334 g mass is connected to a light spring of force constanct 3 N/m and it is free to oscillate on a horizontal, frictionless track. The mass is displaced 4 cm from the equilibrium point and released from rest.A.) Find the period of the motion in units of s.B.) What is the maximum speed of the mass in units of m/s.C.) What is the maximun acceleration of the mass in units of m/s^2.

Answer 1

Step-by-step explanation:

Given that,

Mass, m = 343 g = 0.343 kg

Force constant, k = 3 N/m

Displacement in the mass from equilibrium position is 4 cm

(a) The time period of the mass that oscillates is given by :

`T=2\pi \sqrt{(m)/(k)} \\\\T=2\pi \sqrt{(0.343)/(3)} \\\\T=2.12\ s`

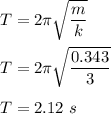
(b) Firstly lets find the angular frequency. It is given by :

`\omega=\sqrt{(k)/(m)} \\\\\omega=\sqrt{(3)/(0.343)} \\\\\omega=2.95\ rad/s`

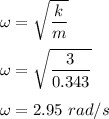
Now the maximum speed of the mass in SHM is given by :

`v=A\omega\\\\v=0.04* 2.95\\\\v=0.118\ m/s`

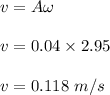
(c) The maximum acceleration of the mass is given by :

`a=A\omega^2\\\\a=0.04* (2.95)^2\\\\a=0.3481\ m/s^2`

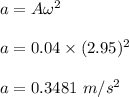
Hence, this is the required solution.