Question

A satellite is in a circular orbit around the Earth. If it is at an altitude equal to twice the radius of the Earth, 2RE, how does its speed v relate to the Earth's radius RE, and the magnitude g of the acceleration due to gravity on the Earth's surface?

Answer 1

Step-by-step explanation:

height of satellite, h = 2 Re

where, Re is the radius of earth

The centripetal force is equal to the gravitational force between the earth and the satellite.

`(mv^(2))/(r)=(GMm)/(r^(2))`

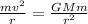
where, m is the mass of satellite and M is the mass of earth, and r is the distance between the centre of earth and the satellite.

r = Re + h = Re + 2Re = 3 Re

`v=\sqrt{(GM)/(r)}`

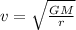
where, G M = gRe²

`v=\sqrt{(gR_(e)^(2))/(3R_(e))}`

`v=\sqrt{(gR_(e))/(3)}`

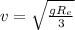
The above expression is the orbital velocity of the satellite at a height.