Question

Krystal's school is selling tickets to annual talent show.On the first day of the ticket sales the school sold 4 senior citizen tickets and 3 student tickets for a total of $25 . The school took in $58 on the second day by selling 4 senior citizen tickets and 14 student tickets find the price of a citizen ticket and the price of a student ticket

Answer 1

$4 is the price of a citizen ticket and $3 is the price of a student ticket.

Explanation:

Given:

Krystal's school is selling tickets to annual talent show.

The total ticket sold on the first day is 4 senior citizen tickets and 3 student tickets for a total of $25.

Now, to find the price of the student ticket and the price of the citizen ticket.

Let the price of a citizen ticket be
`x.`

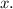
Let the price of a student ticket be
`y.`

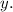
So, the total amount of the first day of the ticket sales:

`4x+3y=25\ \ \ ....(1)`

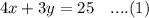
According to question:

The total amount of the second day of the ticket sales:

`4x+14y=58\ \ \ \ .....(2)`

Now, using the elimination method we solve the equation:

So, subtracting equation (1) from equation (2):

`4x+14y-(4x+3y)=58-25\\\\4x+14y-4x-3y=58-25\\\\11y=33`

Dividing both sides by 11 we get:

`y=3.`

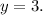
The price of a student ticket = $3.

Now, substituting the value of
`y` in equation (1) we get:

`4x+3y=25\\\\4x+3* 3=25\\\\4x+9=25\\\\Subtracting\ both\ sides\ by\ 9\ we\ get:\\\\4x=16\\\\Dividing\ both\ sides\ by\ 4\ we\ get:\\\\x=4.`

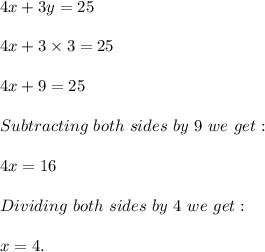
The price of a citizen ticket = $4.

Thus, $4 is the price of a citizen ticket and $3 is the price of a student ticket.