Question

The volume of a number cube is 27 cm^3. What is the length of each side of a cube?

Answer 1

Side = 3 cm

Explanation:

Given:

`\text{Volume of cube} = 27 \ \text{cm}^(3)`

The formula to calculate the volume is (Side)³.

Thus, we obtained the following equation:

`(\text{Side})^(3) = 27 \text{cm}^(3) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ [\text{Side}^(3) = \text{Volume of cube}]`

Cube root both sides to obtain the side length of the cube:

`\implies \sqrt[3]{\text{(Side)}^(3)} = \sqrt[3]{27 \ \text{cm}^(3) }`

Evaluate the side of the cube:

`\implies \sqrt[3]{\text{(Side)}^(3)} = \sqrt[3]{27 \ \text{cm}^(3) }`

`\implies \sqrt[3]{\text{(Side)}\text{(Side)(Side})} = \sqrt[3]{3 * 3 * 3 * \text{(cm)(cm)(cm)}}`

`\implies \text{Side = 3 cm}`

Answer 2

3 cm

Explanation:

Formula

Volume of a cube =
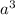`a^3` (where a is the side length)

Given that the volume of the cube is 27 cm³, to find the side length, substitute the given volume into the equation and solve for
`a`:

`\implies 27\: \sf cm^3=a^3`

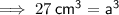
Cube root both sides:

`\implies \sqrt[3]{27\: \sf cm^3} =\sqrt[3]{a^3}`

`\implies \sqrt[3]{27}\sqrt[3]{\sf cm^3} =\sqrt[3]{a^3}`

`\implies 3\: \sf cm=a`

`\implies a=3\: \sf cm`

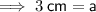
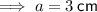
Therefore, the length of each side of the cube is 3 cm.