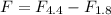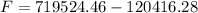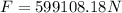Question

A large aquarium of height 5 m is filled with fresh water to a depth of D = 1.80 m. One wall of the aquarium consists of thick plastic with horizontal length w = 7.60 m. By how much does the total force on that wall increase if the aquarium is next filled to a depth of D = 4.40 m? (Note: use g = 9.81 m/s2 and rho = 998 kg/m3.)

Answer 1

To solve the problem we will first start considering the Pressure given the hydrostatic definition of the product between the density, the gravity and the depth. We will define the area where the liquid acts and later we will use the definition of the force as a product between the pressure and the area to calculate the force given in the two depths. The gauge pressure at the depth x will be

`(P-P_a)= \rho g x`

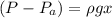
This pressure acts on the strip of area

`dA = 7.6dx`

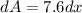
The force acting on that strip is given by,

`dF = (P-P_a)dA`

`dF = \rho g xdA`

`dF = 7.6 \rho g x dx`

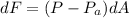
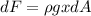
To evaluate the force, we will then consider the integral of the pressure as a function of the Area, or the integral of the previously found terms.

`F = \int_0^x 7.6 \rho g x dx`

`F = 3.8 \rho g x^2`

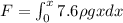
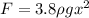
Evaluating at the initial depth of 1.8m and the final depth of 4.4 we have then that,

`F_(1.8) = 3.8 (998)(9.8)(1.8)^2 = 120416.28N`

`F_(4.4) = 3.8(998)(9.8)(4.4)^2 = 719524.46N`

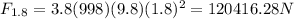
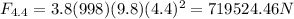
Therefore the Net force will be

`F = F_(4.4)-F_(1.8)`

`F = 719524.46-120416.28`

`F = 599108.18N`