Question

A horizontal spring with spring constant 100N/m is compressed 20cm and used to launch a 2.3kg box across a frictionless, horizontal surface. After the box travels some distance, the surface becomes rough. The coefficient of kinetic friction of the box on the surface is 0.15.Use work and energy to find how far the box slides across the rough surface before stopping.

Answer 1

The box slides 0.58 m before stopping .

Step-by-step explanation:

Given :

Spring constant , k = 100 N/m .

Compression in the spring , x = 20 cm .

Mass of box , m = 2.3 kg .

Coefficient of kinetic friction of the box on the surface is ,
`\mu=0.15` .

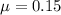Therefore , conserving energy of the system :

`K.E_i+U_i=K.E_f+U_f\\\\(kx^2)/(2)+0=0+\mu( mgx)`

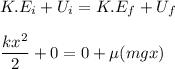
Putting value in above equation we get :

`(100* 0.2^2)/(2)+0=0+0.15* ( 2.3* 10* x)\\\\2=x* 3.45\\x=0.58\ m`

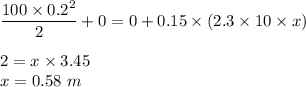
Therefore , the box slides 0.58 m before stopping .