Answer:
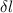 = 0.428 mm
= 0.428 mm
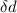 = −0.0145 mm
= −0.0145 mm
Step-by-step explanation:
given data
diameter = 20.9 mm
length = 203 mm
force = 46600 N
elastic modulus = 64.4 GPa
Poisson's ratio = 0.33
solution
we get here first area of cross section that is
Area =
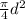 .............1
.............1
put here value and we will get
Area =
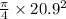
Area = 343.06 mm²
and
now we get here change in direction of applied stress that is
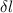 =
=
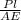 .....................2
.....................2
put here value and we will get
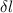 =
=
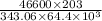
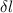 = 0.428 mm
= 0.428 mm
and
we know Poisson ratio will be here express as
m =
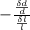 ........................3
........................3
0.33 =

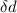 = −0.0145 mm
= −0.0145 mm
so here change in diameter have -ve sign so diameter is decrease.