Answer:
a) 0.239 < p < 0.311.
b) no, the confidence interval include 0.25, so the true percentage could easly equal 25%
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
For this problem, we have that:
163 yellow peas out of 163 + 429 = 592 total peas
So
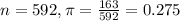
95% confidence level
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
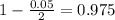 , so
, so
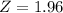 .
.
The lower limit of this interval is:
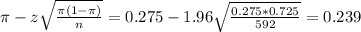
The upper limit of this interval is:
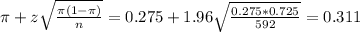
So
A) 0.239 < p < 0.311.
B)
25% is part of the confidence interval.
So the answer is:
no, the confidence interval include 0.25, so the true percentage could easly equal 25%