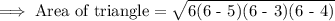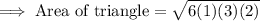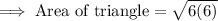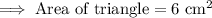Answer:
6 cm²
Explanation:
Since 3 side lengths are given, I assume that this figure is a triangle. The area of a triangle can be determined by using hero's formula.
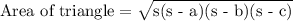
⇒ s = Perimeter/2
⇒ a, b, and c = side lenths of triangle
Replacing a, b, and c as the given side lengths:
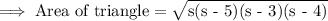
Determining the perimeter of the triangle:

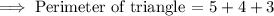
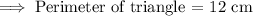
Determining the half of perimeter:
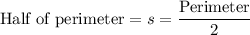
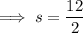
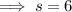
Replacing the value of "s" in the formula:
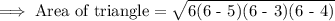
Evaluating the area: